Главная > Редуктор > Решение егэ профиль 7 номер. Подготовка к ЕГЭ по математике (профильный уровень): задания, решения и объяснения. Как будут распределять баллы

Решение егэ профиль 7 номер. Подготовка к ЕГЭ по математике (профильный уровень): задания, решения и объяснения. Как будут распределять баллы

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

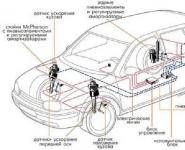
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x 1 , x 2 , …, x 9 . Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

Алгоритм решения:

Рассматриваем график функции.
Ищем точки, в которых функция убывает.
Подсчитываем их количество.
Записываем ответ.

Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x 3 , x 4 , x 5 , x 9 . Таких точек 4.

Второй вариант задания (из Ященко, №4)

Алгоритм решения:

Рассматриваем график функции.
Рассматриваем поведение функции в каждой из точек и знак производной в них.
Находим точки в наибольшим значением производной.
Записываем ответ.

Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Третий вариант задания (из Ященко, №21)

Алгоритм решения:

Приравняем уравнения касательной и функции.
Упрощаем полученное равенство.
Находим дискриминант.
Определяем параметр а , при котором решение единственное.
Записываем ответ.

Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим.

Учитесь замечать грамматические ошибки. Если вы научитесь уверенно распознавать их в задании, то не потеряете баллы в сочинении. (Критерий 9 - «Соблюдение языковых норм».) Кроме того, задание, за которое вы можете получить 5 баллов, требует особого отношения!

Задание 7 ЕГЭ по русскому языку

Формулировка задания: Установите соответствие между грамматическими ошибками и предложениями, в которых они допущены: к каждой позиции первого столбца подберите соответствующую позицию из второго столбца.

Грамматические ошибки

предложения

А) нарушение в построении предложения с причастным оборотомБ) ошибка в построении сложного предложения

В) нарушение в построении предложения с несогласованным приложением

Г) нарушение связи между подлежащим и сказуемым

Д) нарушение видо-временной соотнесённости глагольных форм

1) И.С. Тургенев подвергает Базарова самому сложному испытанию – «испытанию любовью» – и этим раскрыл истинную сущность своего героя.2) Все, кто побывал в Крыму, увёз с собой после расставания с ним яркие впечатления о море, горах, южных травах и цветах.

3) В основе произведения «Повести о настоящем человеке» лежат реальные события, произошедшие с Алексеем Маресьевым.

4) С. Михалков утверждал, что мир купеческого Замоскворечья можно увидеть на сцене Малого театра благодаря великолепной игре актёров.

5) В 1885 году В.Д. Поленов экспонировал на передвижной выставке девяносто семь этюдов, привезённым из поездки на Восток.

6) Теория красноречия для всех родов поэтических сочинений написана А.И. Галичем, преподававшим русскую и латинскую словесность в Царскосельском лицее.

7) В пейзаже И. Машкова «Вид Москвы» есть ощущение звонкой красочности городской улицы.

8) Счастливы те, кто после долгой дороги с её холодом и слякотью видит знакомый дом и слышит голоса родных людей.

9) Читая классическую литературу, замечаешь, что насколько по-разному «град Петров» изображён в произведениях А.С. Пушкина, Н.В. Гоголя, Ф.М. Достоевского.

Запишите в таблицу выбранные цифры под соответствующими буквами.

Как выполнять такое задание? Целесообразнее начинать с левой части. Названное синтаксическое явление (причастный оборот, подлежащие и сказуемое и т. д.) находите в предложениях справа и проверяете, нет ли грамматической ошибки. Начинайте с тех, что легче найти и определить.

Разберем типичные грамматические ошибки в таком порядке, в каком их следует проверять на экзамене.

Несогласованное приложение

Несогласованное приложение – это название книги, журнала, фильма, картины и т. д., заключенное в кавычки.

В предложении изменяется по падежам родовое слово, а несогласованное приложение стоит в начальной форме и не изменяется: в романе «Война и мир»; картину Левитана «Золотая осень», на станции метро «Тверская».

Если родового слова в предложении нет, изменяется по падежам само приложение: герои «Войны и мира»; смотрю на «Золотую осень» Левитана, встретимся на «Тверской».

Грамматическая ошибка: в романе «Войне и мире»; на картине «Золотой осени», на станции метро «Тверской».

В задании такая ошибка встретилась в предложении 3.

Прямая и косвенная речь.

Предложение с косвенной речью представляет собой сложноподчиненное предложение. Сравните:

Проводник сказал: «Я принесу вам чай» - Проводник сказал, что он принесет нам чай. Грамматическая ошибка: Проводник сказал, что я принесу вам чай. (Личное местоимение должно измениться.)

Пассажир спросил: «Могу ли я открыть окно» - Пассажир спросил, может ли он открыть окно. Грамматическая ошибка: Пассажир спросил, что может ли он открыть окно. (В предложении есть ЛИ в роли союза, союз ЧТО недопустим в предложении.)

Причастный оборот

Находим предложения с причастным оборотом, смотрим, нет ли ошибок в его построении.

1. Внутрь причастного оборота не может попасть определяемое (главное) слово, оно может стоять до или после него. Грамматическая ошибка: пришедшие зрители на встречу с режиссером. Правильно: пришедшие на встречу с режиссером зрители или зрители, пришедшие на встречу с режиссером.

2. Причастие должно согласовываться в роде, числе и падеже с главным словом, которое определяется по смыслу и по вопросу: жители гор (какие?), напуганные ураганом или жители гор (каких?),заросших елями. Грамматическая ошибка: жители гор, напуганных ураганом или жители гор, заросшие елями.

Обратите внимание: одно из событий, случившееся прошлым летом (согласуем причастие со словом ОДНО – речь идет об одном событии). Вспоминается ряд событий, случившихся прошлым летом (задаем вопрос от СОБЫТИЙ «каких?»).

3. У причастия есть настоящее время (ученик, запоминающий правило ), прошедшее время (ученик, запомнивший правило ), но нет будущего времени (ученик, запомнящий правило – грамматическая ошибка).

В задании такая ошибка встретилась в предложении 5.

Деепричастный оборот

Запомните : Деепричастие называет добавочное действие, а глагол-сказуемое – основное. Деепричастие и глагол-сказуемое должны относиться к одному действующему лицу!

Находим в предложении подлежащее и проверяем, выполняет ли оно действие, названное деепричастием. Идя на первый бал, у Наташи Ростовой возникло естественное волнение . Рассуждаем: волнение возникло - Наташа Ростова шла – разные действующие лица. Правильный вариант: Идя на первый бал, Наташа Ростова испытывала естественное волнение.

В определенно-личном предложении легко восстановить подлежащее: Я, МЫ, ТЫ, ВЫ: Составляя предложение, учитывайте (вы) грамматическое значение слова . Рассуждаем: вы учитываете и вы составляете – ошибки нет.

Глагол-сказуемое может быть выражен инфинитивом : Составляя предложение, надо учитывать грамматическое значение слова .

Рассуждаем: Прочитав предложение, мне кажется, что ошибки нет. МНЕ не может быть подлежащим, так как стоит не в начальной форме. Данное предложение с грамматической ошибкой.

Грамматическая связь между подлежащим и сказуемым.

Ошибка может скрываться в сложноподчиненных предложениях, построенных по модели «ТЕ, КТО…», «КАЖДЫЙ, КТО…», «ВСЕ, КТО…», «НИКТО ИЗ ТЕХ, КТО…», «МНОГИЕ ИЗ ТЕХ, КТО…», «ОДИН ИЗ ТЕХ, КТО…». В каждом простом предложении в составе сложноподчиненного будет свое подлежащее, надо проверить, согласуются ли они со своими сказуемыми. КТО, КАЖДЫЙ, НИКТО, ОДИН, сочетаются со сказуемыми в единственном числе; ТЕ, ВСЕ, МНОГИЕ сочетаются со своими сказуемыми во множественном числе.

Анализируем предложение: Никто из тех, кто побывал там летом, не были разочарованы. НИКТО НЕ БЫЛИ – грамматическая ошибка. КТО ПОБЫВАЛ – ошибки нет. Те, кто не пришли на открытие выставки, об этом пожалели. ТЕ ПОЖАЛЕЛИ – ошибки нет. КТО НЕ ПРИШЛИ – грамматическая ошибка.

В задании такая ошибка встретилась в предложении 2.

Нарушение видовременной соотнесенности глагольных форм.

Обратите особое внимание на глаголы-сказуемые: неправильное употребление времени глагола ведет к путанице в последовательности действий. Я работаю невнимательно, с остановками, а в результате сделал много нелепых ошибок. Исправим ошибку: Я работаю невнимательно, с остановками, а в результате делаю много нелепых ошибок. (Оба глагола несовершенного вида стоят в настоящем времени.) Я работал невнимательно, с остановками, а в результате сделал много нелепых ошибок. (Оба глагола стоят в прошедшем времени, первый глагол - несовершенного вида - указывает на процесс, второй – совершенного вида – указывает на результат.)

В задании такая ошибка встретилась в предложении 1: Тургенев подвергает и раскрыл...

Однородные члены предложения

Грамматические ошибки в предложениях с союзом И .

Союз И не может связывать один из членов предложения с целым предложением. Я не люблю болеть и когда получаю двойку . Москва – город, который был родиной Пушкина и подробно описанный им. Когда Онегин вернулся в Петербург и встретив Татьяну, он не узнал её. Слушали лекцию о значении спорта и почему им нужно заниматься . (Исправим ошибку: Слушали лекцию о значении спорта и о пользе спортивных занятий . Или: Слушали лекцию о том, какое значение имеет спорт и почему им нужно заниматься .)
Союз И не может связывать однородные члены, выраженные полной и краткой формой прилагательных и причастий: Он высок и худощавый. Она умная и красива.
Союз И не может связывать инфинитив и существительное: Я люблю стирать, готовить и чтение книг . (Правильно: Я люблю стирать, готовить и читать книги. )
Трудно распознать ошибку в такой синтаксической конструкции: Декабристы любили и восхищались русским народом. В этом предложении дополнение НАРОДОМ относится к обоим сказуемым, но грамматически связано только с одним из них: ВОСХИЩАЛИСЬ (КЕМ?) НАРОДОМ. От глагола ЛЮБИЛИ задаем вопрос КОГО? Обязательно задавайте вопрос от каждого глагола-сказуемого к дополнению. Вот типичные ошибки: родители заботятся и любят детей; я понимаю и сочувствую тебе; он изучил и пользовался правилом; я люблю и горжусь сыном. Исправление такой ошибки требует введения разных дополнений, каждое будет согласовываться со своим глаголом-сказуемым: Я люблю сына и горжусь им.

Использование составных союзов .

Учитесь распознавать в предложении следующие союзы: «НЕ ТОЛЬКО…, НО И»; «КАК…, ТАК И». В этих союзах нельзя пропускать отдельные слова или заменять их другими: Не только мы, но наши гости были удивлены. Атмосферу эпохи в комедии создают не только действующие лица, а также внесценические персонажи. Как и днем, так и ночью кипит работа.
Части двойного союза должны находиться непосредственно перед каждым из однородных членов. Неправильный порядок слов ведет к грамматической ошибке: Мы осмотрели не только древнюю часть города, но и побывали в новых районах. (Правильный порядок: Мы не только осмотрели…, но и побывали… ) В сочинении надо как о главных героях , так и рассказать о художественных особенностях . (Правильный порядок: В сочинении надо рассказать как о главных героях , так и о художественных особенностях. )

Обобщающие слова при однородных членах

Обобщающее слово и следующие за ним однородные члены стоят в одном и том же падеже: Занимайся двумя видами спорта: (чем?) лыжами и плаваньем. (Грамматическая ошибка: Сильные люди обладают двумя качествами: доброта и скромность.)

Предлоги при однородных членах

Предлоги перед однородными членами можно опускать только в том случае, если эти предлоги одинаковы: Он побывал в Греции, Испании, Италии, на Кипре. Грамматическая ошибка: Он побывал в Греции, Испании, Италии, Кипре.

Сложноподчиненное предложение

Очень распространены ошибки, связанные с неправильным использованием союзов, союзных слов, указательных слов. Вариантов ошибок может быть много, рассмотрим некоторые из них.

Лишний союз: Меня мучил вопрос, что надо ли всё рассказать отцу. Я не подумал, что насколько я был далек от истины.

Смешение сочинительных и подчинительных союзов: Когда Мурке надоедало возиться с котятами, и она уходила куда-нибудь поспать.

Лишняя частица БЫ: Надо, чтобы он зашел бы ко мне.

Отсутствует указательное слово: Ваша ошибка заключается, что вы слишком торопитесь. (Пропущено В ТОМ.)

Союзное слово КОТОРЫЙ оторвано от определяемого слова: Теплый дождик смочил землю, в котором так нуждались растения. (Правильно: Теплый дождик, в котором нуждались растения, смочил землю.)

В задании такая ошибка допущена в предложении 9.

Неправильное употребление падежной формы существительного с предлогом

1. Предлоги БЛАГОДАРЯ, СОГЛАСНО, ВОПРЕКИ, НАПЕРЕРЕЗ, НАПЕРЕКОР, ПОДОБНО + существительное в ДАТЕЛЬНОМ ПАДЕЖЕ: благодаря умени ю , согласно расписани ю , вопреки правил ам .

Предлог ПО может употребляться в значении «ПОСЛЕ». В этом случае существительное стоит в предложном падеже и имеет окончание И: по окончании школы (после окончания), по приезде в город (после приезда), по истечении срока (после истечения срока).

Запомните : по прибытиИ , по окончаниИ , по завершениИ , по истечениИ , по приездЕ , по прилетЕ .

Запоминаем особенности управления в следующих словосочетаниях:

Доказывать (что?) правоту

Поражаться (чему?) терпению

Привести пример (чего?) ошибки

Подвести итог (чему?) работе

Признаться (в чём?) в преступлении

Скучать, грустить (по ком?) по вас

Уделять внимание (чему?) мелочам

Указывать (на что?) на недостатки

Упрекать (в чём?) в жадности

Запоминаем пары:

Беспокоиться о сыне – тревожиться за сына

Верить в победу – уверенность в победе

Вопрос о строительстве – проблемы со строительством

Извлекать доход из аренды – получать доход с аренды

Неосведомленность в проблеме – незнакомство с проблемой

Обидеться на недоверие – обидеть недоверием

Обращать внимание на здоровье – уделять внимание здоровью

Озабоченность делами – тревога о делах

Оплатить проезд – заплатить за проезд

Отзыв о сочинении – рецензия на сочинение

Плата за услугу – оплата услуги

Превосходство над ним – преимущество перед ним

Предостеречь от опасности – предупредить об опасности

Различать друзей и врагов – отличать друзей от врагов

Удивляться терпению – удивлен терпением

Характерно для него – присуще ему

Программа экзамена, как и в прошлые годы, составлена из материалов основных математических дисциплин. В билетах будут присутствовать и математические, и геометрические, и алгебраические задачи.

Изменений в КИМ ЕГЭ 2020 по математике профильного уровня нет.

Особенности заданий ЕГЭ по математике-2020

Осуществляя подготовку к ЕГЭ по математике (профильной), обратите внимание на основные требования экзаменационной программы. Она призвана проверить знания углубленной программы: векторные и математические модели, функции и логарифмы, алгебраические уравнения и неравенства.
Отдельно потренируйтесь решать задания по .
Важно проявить нестандартность мышления.

Структура экзамена

Задания ЕГЭ профильной математики разделены на два блока.

Часть - краткие ответы , включает 8 задач, проверяющих базовую математическую подготовку и умение применять знания по математике в повседневности.
Часть - краткие и развернутые ответы . Состоит из 11 задач, 4 из которых требуют короткого ответа, и 7 – развернутого с аргументацией выполненных действий.

Повышенной сложности - задания 9-17 второй части КИМа.
Высокого уровня сложности - задачи 18-19 –. Эта часть экзаменационных заданий проверяет не только уровень математических знаний, но и наличие или отсутствие творческого подхода к решению сухих «циферных» заданий, а также эффективность умения использовать знания и навыки в качестве профессионального инструмента.

Важно! Поэтому при подготовке к ЕГЭ теорию по математике всегда подкрепляйте решением практических задач.

Как будут распределять баллы

Задания части первой КИМов поматематике близки к тестам ЕГЭ базового уровня, поэтому высокого балла на них набрать невозможно.

Баллы за каждое задание по математике профильного уровня распределились так:

за правильные ответы на задачи №1-12 – по 1 баллу;
№13-15 – по 2;
№16-17 – по 3;
№18-19 – по 4.

Длительность экзамена и правила поведения на ЕГЭ

Для выполнения экзаменационной работы-2020 ученику отведено 3 часа 55 минут (235 минут).

В это время ученик не должен:

вести себя шумно;
использовать гаджеты и другие технические средства;
списывать;
пытаться помогать другим, или просить помощи для себя.

За подобные действия экзаменующегося могут выдворить из аудитории.

На государственный экзамен по математике разрешено приносить с собой только линейку, остальные материалы вам выдадут непосредственно перед ЕГЭ. выдаются на месте.

Эффективная подготовка - это решение онлайн тестов по математике 2020. Выбирай и получай максимальный балл!

Представляю решение 7 задания ОГЭ-2016 по информатике из проекта демоверсии. По сравнению с демоверсией 2015 года, 7 задание не изменилось. Это задание на умение кодировать и декодировать информацию (Кодирование и декодирование информации). Ответом к заданию 7 является последовательность букв, которую следует записать в поле ответа.

Скриншот 7 задания.

Задание:

Разведчик передал в штаб радиограмму
– – – – – – – –
В этой радиограмме содержится последовательность букв, в которой встречаются только буквы А, Д, Ж, Л, Т. Каждая буква закодирована с помощью азбуки Морзе. Разделителей между кодами букв нет. Запишите в ответе переданную последовательность букв.
Нужный фрагмент азбуки Морзе приведён ниже.

Ответ: __

Такое задание лучше всего решать последовательно, закрывая каждый возможный код.
1. ( –) – – – – – – –, первые две позиции могут быть только буквой А
2.
а) ( –) (– ) – – – – – –, следующие три позиции могут быть буквой Д
б) ( –) (–) – – – – – –, или одна позиция буква Л, но если взять следующую комбинацию ( –) (–) ( –) – – – – –, (буква Т) то больше выбрать мы не сможем (таких сочетаний начинающихся с двух точек просто нет), т.о. мы зашли в тупик и делаем вывод, что этот путь неправильный
3. Возвращаемся к варианту а)
( –) (– ) ( – ) – – – – –, это буква Ж
4. ( –) (– ) ( – ) (–) – – – –, это буква Л
5. ( –) (– ) ( – ) (–) (– ) – – –, это буква Д
6. ( –) (– ) ( – ) (–) (– ) (–) – –, и это буква Л
7. ( –) (– ) ( – ) (–) (– ) (–) ( –) –, буква А
8. ( –) (– ) ( – ) (–) (– ) (–) ( –) (–), буква Л
9. Собираем все буквы, которые у нас получились: АДЖЛДЛАЛ .

Ответ: АДЖЛДЛАЛ

1. а) $\frac{\pi }{2}+\pi k; \, \pm \frac{2\pi }{3}+2\pi k;\, k\in \mathbb{Z} $
  б) $\frac{9\pi }{2};\frac{14\pi }{3};\frac{16\pi }{3};\frac{11\pi }{2} $ а) Решите уравнение $2\sin \left (2x+\frac{\pi }{6} \right)+ \cos x =\sqrt{3}\sin (2x)-1 $.
  б) Найдите его решения, принадлежащие промежутку $\left $.
2. а) $\frac{\pi }{2}+\pi k; \, \pm \frac{\pi }{3}+2\pi k;\, k\in \mathbb{Z} $
  б) $\frac{5\pi }{2};\frac{7\pi }{2};\frac{11\pi }{3} $ а) Решите уравнение $2\sin \left (2x+\frac{\pi }{6} \right)-\cos x =\sqrt{3}\sin (2x)-1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [\frac{5\pi }{2}; 4\pi\right ] $.
3. а)
  б) $-\frac{5\pi }{2};-\frac{3\pi }{2};-\frac{5\pi }{4} $ а) Решите уравнение $\sqrt{2}\sin\left (2x+\frac{\pi }{4} \right)+\sqrt{2}\cos x= \sin (2x)-1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [-\frac{5\pi }{2}; -\pi \right ] $.
4. а) $\frac{\pi }{2}+\pi k; \, \pm \frac{5\pi }{6}+2\pi k;\, k\in \mathbb{Z} $
  б) $\frac{7\pi }{6};\frac{3\pi }{2};\frac{5\pi }{2} $ а) Решите уравнение $\sqrt{2}\sin\left (2x+\frac{\pi }{4} \right)+\sqrt{3}\cos x= \sin (2x)-1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ \pi; \frac{5\pi }{2} \right ] $.
5. а) $\pm \frac{\pi }{2}+2\pi k; \pm \frac{2\pi }{3}+2\pi k,k\in \mathbb{Z} $
  б) $-\frac{11\pi }{2}; -\frac{16\pi }{3}; -\frac{14\pi }{3}; -\frac{9\pi }{2} $ а) Решите уравнение $\sqrt{2}\sin\left (2x+\frac{\pi }{4} \right)+\cos x= \sin (2x)-1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [-\frac{11\pi }{2}; -4\pi \right ] $.
6. а) $\frac{\pi }{2}+\pi k; \, \pm \frac{\pi }{6}+2\pi k;\, k\in \mathbb{Z} $
  б) $-\frac{23\pi }{6};-\frac{7\pi }{2};-\frac{5\pi }{2} $ а) Решите уравнение $2\sin\left (2x+\frac{\pi }{3} \right)-3\cos x= \sin (2x)-\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left [-4\pi; -\frac{5\pi }{2} \right ] $.
7. а) $\frac{\pi }{2}+\pi k; \, \pm \frac{3\pi }{4}+2\pi k;\, k\in \mathbb{Z} $
  б) $\frac{13\pi }{4};\frac{7\pi }{2};\frac{9\pi }{2} $ а) Решите уравнение $2\sin \left (2x+\frac{\pi }{3} \right)+\sqrt{6}\cos x=\sin (2x)-\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left $.
1. а) $(-1)^k \cdot \frac{\pi}{4} +\pi k, k\in \mathbb{Z} $
  б) $-\frac{13\pi}{4} $ а) Решите уравнение $\sqrt{2}\sin x+2\sin\left (2x-\frac{\pi}{6} \right)=\sqrt{3}\sin(2x)+1 $.
  б)
2. а)
  б) $2\pi; 3\pi; \frac{7\pi}{4} $ а) Решите уравнение $\sqrt{2}\sin\left (2x+\frac{\pi}{4} \right)-\sqrt{2}\sin x=\sin(2x)+1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ \frac{3\pi}{2}; 3\pi \right ] $.
3. а) $\pi k, (-1)^k \cdot \frac{\pi}{3} +\pi k, k\in \mathbb{Z} $
  б) $-3\pi; -2\pi; -\frac{5\pi}{3} $ а) Решите уравнение $\sqrt{3}\sin x+2\sin\left (2x+\frac{\pi}{6} \right)=\sqrt{3}\sin(2x)+1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -3\pi ; -\frac{3\pi}{2}\right ] $.
4. а) $\pi k; (-1)^{k} \cdot \frac{\pi}{6}+\pi k; k\in \mathbb{Z} $
  б) $-\frac{19\pi }{6}; -3\pi ; -2\pi $ а) Решите уравнение $\sin x+2\sin\left (2x+\frac{\pi}{6} \right)=\sqrt{3}\sin(2x)+1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -\frac{7\pi}{2}; -2\pi \right ] $.
5. а) $\pi k; (-1)^{k+1} \cdot \frac{\pi}{6}+\pi k; k\in \mathbb{Z} $
  б) $\frac{19\pi }{6}; 3\pi ; 2\pi $ а) Решите уравнение $2\sin \left (2x+\frac{\pi }{3} \right)-\sqrt{3}\sin x = \sin (2x)+\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left $.
6. а) $\pi k; (-1)^{k+1} \cdot \frac{\pi}{4} +\pi k, k\in \mathbb{Z} $
  б) $-3\pi; -\frac{11\pi}{4}; -\frac{9\pi}{4}; -2\pi $ а) Решите уравнение $\sqrt{6}\sin x+2\sin \left (2x-\frac{\pi }{3} \right) = \sin (2x)-\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -\frac{7\pi}{2};-2\pi \right ] $.
1. а) $\pm \frac{\pi}{2}+2\pi k; \pm \frac{2\pi}{3}+2\pi k,k\in \mathbb{Z} $
  б) $\frac{7\pi}{2};\frac{9\pi}{2};\frac{14\pi}{3} $ а) Решите уравнение $\sqrt{2}\sin(x+\frac{\pi}{4})+\cos(2x)=\sin x -1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ \frac{7\pi}{2}; 5\pi \right ]$.
2. а) $\pm \frac{\pi }{2}+2\pi k; \pm \frac{5\pi }{6} +2\pi k, k\in \mathbb{Z} $
  б) $-\frac{3\pi}{2};-\frac{5\pi}{2} ;-\frac{17\pi}{6} $ а) Решите уравнение $2\sin(x+\frac{\pi}{3})+\cos(2x)=\sin x -1 $.
  б)
3. а) $\frac{\pi}{2}+\pi k; \pm \frac{\pi}{3} +2\pi k,k\in \mathbb{Z} $
  б) $-\frac{5\pi}{2};-\frac{5\pi}{3};-\frac{7\pi}{3} $ а) Решите уравнение $2\sin(x+\frac{\pi}{3})-\sqrt{3}\cos(2x)=\sin x +\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -3\pi;-\frac{3\pi}{2} \right ] $.
4. а) $\frac{\pi}{2}+\pi k; \pm \frac{\pi}{4} +2\pi k,k\in \mathbb{Z} $
  б) $\frac{5\pi}{2};\frac{7\pi}{2};\frac{15\pi}{4} $ а) Решите уравнение $2\sqrt{2}\sin(x+\frac{\pi}{6})-\cos(2x)=\sqrt{6}\sin x +1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [\frac{5\pi}{2}; 4\pi; \right ] $.
1. а) $(-1)^{k+1} \cdot \frac{\pi }{3}+\pi k ; \pi k, k\in \mathbb{Z} $
  б) $\frac{11\pi }{3}; 4\pi ; 5\pi $ а) Решите уравнение $\sqrt{6}\sin\left (x+\frac{\pi }{4} \right)-2\cos^{2} x=\sqrt{3}\cos x-2 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ \frac{7\pi }{2};5\pi \right ] $.
2. а) $\pi k; (-1)^k \cdot \frac{\pi }{4}+\pi k, k\in \mathbb{Z} $
  б) $-3\pi; -2\pi; -\frac{7\pi}{4} $ а) Решите уравнение $2\sqrt{2}\sin\left (x+\frac{\pi }{3} \right)+2\cos^{2} x=\sqrt{6}\cos x+2 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -3\pi ; \frac{-3\pi }{2} \right ] $.
3. а) $\frac{3\pi}{2}+2\pi k, \frac{\pi}{6}+2\pi k, \frac{5\pi}{6}+2\pi k, k\in \mathbb{Z} $
  б) $-\frac{5\pi}{2};-\frac{11\pi}{6} ;-\frac{7\pi}{6} $ а) Решите уравнение $2\sin\left (x+\frac{\pi}{6} \right)-2\sqrt{3}\cos^2 x=\cos x -\sqrt{3} $.
  б)
4. а) $2\pi k; \frac{\pi}{2}+\pi k,k\in \mathbb{Z} $
  б) $-\frac{7\pi}{2};;-\frac{5\pi}{2}; -4\pi $ а) Решите уравнение $\cos^2 x + \sin x=\sqrt{2}\sin\left (x+\frac{\pi}{4} \right) $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -4\pi; -\frac{5\pi}{2} \right ]$.
5. а) $\pi k; (-1)^{k+1} \cdot \frac{\pi}{6}+\pi k, k\in \mathbb{Z} $
  б) $-2\pi; -\pi ;-\frac{13\pi}{6} $ а) Решите уравнение $2\sin\left (x+\frac{\pi}{6} \right)-2\sqrt{3}\cos^2 x=\cos x -2\sqrt{3} $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -\frac{5\pi}{2};-\pi \right ] $.
1. а) $\pi k; - \frac{\pi}{6}+2\pi k; -\frac{5\pi}{6} +2\pi k,k\in \mathbb{Z} $
  б) $-\frac{5\pi}{6};-2\pi; -\pi $ а) Решите уравнение $2\sin^2 x+\sqrt{2}\sin\left (x+\frac{\pi}{4} \right)=\cos x $.
  б)
2. а) $\pi k; \frac{\pi}{4}+2\pi k; \frac{3\pi}{4} +2\pi k,k\in \mathbb{Z} $
  б) $\frac{17\pi}{4};3\pi; 4\pi $ а) Решите уравнение $\sqrt{6}\sin^2 x+\cos x =2\sin\left (x+\frac{\pi}{6} \right) $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -2\pi;-\frac{\pi}{2} \right ]$.
1. а) $\pi k; \pm \frac{\pi}{3} +\pi k, k\in \mathbb{Z} $
  б) $3\pi; \frac{10\pi}{3};\frac{11\pi}{3};4\pi; \frac{13\pi}{3} $ а) Решите уравнение $4\sin^3 x=3\cos\left (x-\frac{\pi}{2} \right) $.
  б) Найдите его решения, принадлежащие промежутку $\left [ 3\pi; \frac{9\pi}{2} \right ] $.
2. а)
  б) $\frac{5\pi}{2}; \frac{11\pi}{4};\frac{13\pi}{4};\frac{7\pi}{2};\frac{15\pi}{4} $ а) Решите уравнение $2\sin^3 \left (x+\frac{3\pi}{2} \right)+\cos x=0 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ \frac{5\pi}{2}; 4\pi \right ] $.
1. а) $\frac{\pi}{2} +\pi k, \pm \frac{\pi}{4} +\pi k, k\in \mathbb{Z} $
  б) $-\frac{15\pi}{4};-\frac{7\pi}{2};-\frac{13\pi}{4};-\frac{11\pi}{4};-\frac{5\pi}{2}; $ а) Решите уравнение $2\cos^3 x=\sin \left (\frac{\pi}{2}-x \right) $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -4\pi; -\frac{5\pi}{2} \right ] $.
2. а) $\pi k, \pm \frac{\pi}{6} +\pi k, k\in \mathbb{Z} $
  б) $-\frac{19\pi}{6};-3\pi; -\frac{17\pi}{6};-\frac{13\pi}{6};-2\pi; $ а) Решите уравнение $4\cos^3\left (x+\frac{\pi}{2} \right)+\sin x=0 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -\frac{7\pi}{2}; -2\pi \right ] $.
1. а) $\frac{\pi}{2}+\pi k; \frac{\pi}{4} +\pi k,k\in \mathbb{Z} $
  б) $-\frac{7\pi}{2};-\frac{11\pi}{4};-\frac{9\pi}{4} $ а) Решите уравнение $\sin 2x+2\sin\left (2x-\frac{\pi}{6} \right)=\sqrt{3}\sin(2x)+1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -\frac{7\pi}{2}; -2\pi \right ] $.
1. а) $\pi k; (-1)^k \cdot \frac{\pi}{6} +\pi k, k\in \mathbb{Z} $
  б) $-3\pi; -2\pi; -\frac{11\pi}{6} $ а) Решите уравнение $2\sin\left (x+\frac{\pi}{3} \right)+\cos(2x)=1+\sqrt{3}\cos x $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -3\pi;-\frac{3\pi}{2} \right ] $.
2. а) $\pi k; (-1)^{k+1} \cdot \frac{\pi}{3} +\pi k, k\in \mathbb{Z} $
  б) $-3\pi;-\frac{8\pi}{3};-\frac{7\pi}{3}; -2\pi $ а) Решите уравнение $2\sqrt{3}\sin\left (x+\frac{\pi}{3} \right)-\cos(2x)=3\cos x -1 $.
  б) Найдите его решения, принадлежащие промежутку $\left [ -3\pi;-\frac{3\pi}{2} \right ] $.

14 : Углы и расстояния в пространстве

1. $\frac{420}{29}$
  а)
  б) Найдите расстояние от точки $B$ до прямой $AC_1 $, если $AB=21, B_1C_1=16, BB_1=12 $.
2. 12
  а) Докажите, что угол $ABC_1 $ прямой.
  б) Найдите расстояние от точки $B$ до прямой $AC_1 $, если $AB=15, B_1C_1=12, BB_1=16 $.
3. $\frac{120}{17}$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что угол $ABC_1 $ прямой.
  б) Найдите расстояние от точки $B$ до прямой $AC_1 $, если $AB=8, B_1C_1=9, BB_1=12 $.
4. $\frac{60}{13}$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что угол $ABC_1 $ прямой.
  б) Найдите расстояние от точки $B$ до прямой $AC_1 $, если $AB=12, B_1C_1=3, BB_1=4 $.
1. $\arctan \frac{17}{6}$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что угол $ABC_1 $ прямой.
  б) Найдите угол между прямой $AC_1 $и $BB_1 $, если $AB=8, B_1C_1=15, BB_1=6 $.
2. $\arctan \frac{2}{3}$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что угол $ABC_1 $ прямой.
  б) Найдите угол между прямой $AC_1 $и $BB_1 $, если $AB=6, B_1C_1=8, BB_1=15 $.
1. 7.2 В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а)
  б) Найдите расстояние между прямыми $AC_1$ и $BB_1$, если $AB = 12, B_1C_1 = 9, BB_1 = 8$.
2. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите расстояние между прямыми $AC_1$ и $BB_1$, если $AB = 3, B_1C_1 = 4, BB_1 = 1$.
1. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите площадь боковой поверхности цилиндра, если $AB = 6, B_1C_1 = 8, BB_1 = 15$.
1. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите площадь полной поверхности цилиндра, если $AB = 6, B_1C_1 = 8, BB_1 = 15$.
1. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите объём цилиндра, если $AB = 6, B_1C_1 = 8, BB_1 = 15$.
2. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите объём цилиндра, если $AB = 7, B_1C_1 = 24, BB_1 = 10$.
3. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ и $B$, а на окружности другого основания - точки $B_1 $ и $C_1 $, причем $BB_1 $- образующая цилиндра, а отрезок $AC_1 $ пересекает ось цилиндра.
  а) Докажите, что прямые $AB$ и $B_1C_1$ перпендикулярны.
  б) Найдите объём цилиндра, если $AB = 21, B_1C_1 = 15, BB_1 = 20$.
1. $\sqrt{5}$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ , $B$ и $C$, а на окружности другого основания – точка $C_1$, причем $CC_1$ – образующая цилиндра, а $AC$ – диаметр основания. Известно, что угол $ACB$ равен 30 градусам.
  а) Докажите, что угол между прямыми $AC_1$ и $BC_1$ равен 45 градусам.
  б) Найдите расстояние от точки B до прямой $AC_1$, если $AB = \sqrt{6}, CC_1 = 2\sqrt{3}$.
1. $4\pi$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ , $B$ и $C$, а на окружности другого основания – точка $C_1$, причем $CC_1$ – образующая цилиндра, а $AC$ – диаметр основания. Известно, что угол $ACB$ равен 30°, $AB = \sqrt{2}, CC_1 = 2$.
  а) Докажите, что угол между прямыми $AС_1$ и $BC_1$ равен 45 градусам.
  б) Найдите объём цилиндра.
2. $16\pi$ В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки $A$ , $B$ и $C$, а на окружности другого основания – точка $C_1$, причем $CC_1$ – образующая цилиндра, а $AC$ – диаметр основания. Известно, что угол $ACB$ равен 45°, $AB = 2\sqrt{2}, CC_1 = 4$.
  а) Докажите, что угол между прямыми $AC_1$ и $BC$ равен 60 градусам.
  б) Найдите объём цилиндра.
1. $2\sqrt{3}$ В кубе $ABCDA_1B_1C_1D_1$ все ребра равны 6.
  а) Докажите, что угол между прямыми $АС$ и $BD_1$ равен 60°.
  б) Найдите расстояние между прямыми $АС$ и $BD_1$.
1. $\frac{3\sqrt{22}}{5} $
  а)
  б) Найдите $QP$, где $P$ – точка пересечения плоскости $MNK$ и ребра $SC$, если $AB=SK=6 $ и $SA=8$.
1. $\frac{24\sqrt{39}}{7} $ В правильной пирамиде $SABC$ точки $M$ и $N$ – середины ребер $AB$ и $BC$ соответственно. На боковом ребре $SA$ отмечена точка $K$. Сечение пирамиды плоскостью $MNK$ является четырехугольником, диагонали которого пересекаются в точке $Q$.
  а) Докажите, что точка $Q$ лежит на высоте пирамиды.
  б) Найдите объём пирамиды $QMNB$, если $AB=12,SA=10 $ и $SK=2$.
1. $\arctan 2\sqrt{11} $ В правильной пирамиде $SABC$ точки $M$ и $N$ – середины ребер $AB$ и $BC$ соответственно. На боковом ребре $SA$ отмечена точка $K$. Сечение пирамиды плоскостью $MNK$ является четырехугольником, диагонали которого пересекаются в точке $Q$.
  а) Докажите, что точка $Q$ лежит на высоте пирамиды.
  б) Найдите угол между плоскостями $MNK$ и $ABC$, если $AB=6, SA=12 $ и $SK=3$.
1. $\frac{162\sqrt{51}}{25} $ В правильной пирамиде $SABC$ точки $M$ и $N$ – середины ребер $AB$ и $BC$ соответственно. На боковом ребре $SA$ отмечена точка $K$. Сечение пирамиды плоскостью $MNK$ является четырехугольником, диагонали которого пересекаются в точке $Q$.
  а) Докажите, что точка $Q$ лежит на высоте пирамиды.
  б) Найдите площадь сечения пирамиды плоскостью $MNK$, если $AB=12, SA=15 $ и $SK=6$.

15 : Неравенства

1. $(-\infty ;-12]\cup \left (-\frac{35}{8};0 \right ]$ Решите неравенство $\log _{11} (8x^2+7)-\log _{11} \left (x^2+x+1\right)\geq \log _{11} \left (\frac{x}{x+5}+7 \right) $.
2. $(-\infty ;-50]\cup \left (-\frac{49}{8};0 \right ]$ Решите неравенство $\log _{5} (8x^2+7)-\log _{5} \left (x^2+x+1\right)\geq \log _{5} \left (\frac{x}{x+7}+7 \right) $.
3. $(-\infty;-27]\cup \left (-\frac{80}{11};0 \right ]$ Решите неравенство $\log _7 (11x^2+10)-\log _7 \left (x^2+x+1\right)\geq \log _7 \left (\frac{x}{x+8}+10 \right) $.
4. $(-\infty ;-23]\cup \left (-\frac{160}{17};0 \right ]$ Решите неравенство $\log _2 (17x^2+16)-\log _2 \left (x^2+x+1\right)\geq \log _2 \left (\frac{x}{x+10}+16 \right) $.
1. $\left [\frac{\sqrt{3}}{3}; +\infty \right) $ Решите неравенство $2\log _2 (x\sqrt{3})-\log _2 \left (\frac{x}{x+1}\right)\geq \log _2 \left (3x^2+\frac{1}{x} \right) $.
2. $\left (0; \frac{1}{4} \right ]\cup \left [\frac{1}{\sqrt{3}};1 \right) $ Решите неравенство $2\log_3(x\sqrt{3})-\log_3\left (\frac{x}{1-x} \right)\leq \log_3 \left (9x^{2}+\frac{1}{x}-4 \right) $.
3. $\left (0; \frac{1}{5} \right ]\cup \left [ \frac{\sqrt{2}}{2}; 1 \right) $ Решите неравенство $2\log_7(x\sqrt{2})-\log_7\left (\frac{x}{1-x} \right)\leq \log_7 \left (8x^{2}+\frac{1}{x}-5 \right) $.
4. $\left (0; \frac{1}{\sqrt{5}} \right ]\cup \left [\frac{1}{2};1 \right) $ Решите неравенство $2\log_2(x\sqrt{5})-\log_2\left (\frac{x}{1-x} \right)\leq \log_2 \left (5x^{2}+\frac{1}{x}-2 \right) $.
5. $\left (0; \frac{1}{3} \right ]\cup \left [\frac{1}{2};1 \right) $ Решите неравенство $2\log_5(2x)-\log_5\left (\frac{x}{1-x} \right)\leq \log_5 \left (8x^{2}+\frac{1}{x}-3 \right) $.
1. $(0; 1] \cup \cup \left $ Решите неравенство $\log _5 (4-x)+\log _5 \left (\frac{1}{x}\right)\leq \log _5 \left (\frac{1}{x}-x+3 \right) $.
1. $(1; 1.5] \cup \cup \cup [ 3.5;+\infty) $ Решите неравенство $\log _5 (x^2+4)-\log _5 \left (x^2-x+14\right)\geq \log _5 \left (1-\frac{1}{x} \right) $.
2. $(1; 1.5] \cup [ 4;+\infty) $ Решите неравенство $\log _3 (x^2+2)-\log _3 \left (x^2-x+12\right)\geq \log _3 \left (1-\frac{1}{x} \right) $.
3. $\left (\frac{1}{2}; \frac{2}{3} \right ] \cup \left [ 5; +\infty \right) $ Решите неравенство $\log _2 (2x^2+4)-\log _2 \left (x^2-x+10\right)\geq \log _2 \left (2-\frac{1}{x} \right) $.
1. $(-3; -2]\cup $ Решите неравенство $\log_2 \left (\frac{3}{x}+2 \right)-\log_2(x+3)\leq \log_2\left (\frac{x+4}{x^2} \right) $.
2. $[-2; -1)\cup (0; 9] $ Решите неравенство $\log_5 \left (\frac{2}{x}+2 \right)-\log_5(x+3)\leq \log_5\left (\frac{x+6}{x^2} \right) $.
1. $\left (\frac{\sqrt{6}}{3};1 \right)\cup \left (1; +\infty \right)$ Решите неравенство $\log _5 (3x^2-2)-\log _5 x
2. \(\left (\frac{2}{5}; +\infty \right)$ Решите неравенство $\log_3 (25x^2-4) -\log_3 x \leq \log_3 \left (26x^2+\frac{17}{x}-10 \right) $.
3. $\left (\frac{5}{7}; +\infty \right)$ Решите неравенство $\log_7 (49x^2-25) -\log_7 x \leq \log_7 \left (50x^2-\frac{9}{x}+10 \right) $.
1. $\left [ -\frac{1}{6}; -\frac{1}{24} \right)\cup (0;+\infty) $ Решите неравенство $\log_5(3x+1)+\log_5 \left (\frac{1}{72x^{2}}+1 \right)\geq \log_5 \left (\frac{1}{24x}+1 \right) $.
2. $\left [ -\frac{1}{4}; -\frac{1}{16} \right)\cup (0;+\infty) $ Решите неравенство $\log_3(2x+1)+\log_3 \left (\frac{1}{32x^{2}}+1 \right)\geq \log_3 \left (\frac{1}{16x}+1 \right) $.
1. $1$ Решите неравенство $\log _2 (3-2x)+2\log _2 \left (\frac{1}{x}\right)\leq \log _2 \left (\frac{1}{x^{2}}-2x+2 \right) $.
2. $(1; 3] $ Решите неравенство $\log _2 (x-1)+\log _2 \left (2x+\frac{4}{x-1}\right)\geq 2\log _2 \left (\frac{3x-1}{2} \right) $.
3. $\left [ \frac{1+\sqrt{5}}{2}; +\infty \right) $ Решите неравенство $\log _2 (x-1)+\log _2 \left (x^2+\frac{1}{x-1}\right)\leq 2\log _2 \left (\frac{x^2+x-1}{2} \right) $.
4. $\left [ 2; +\infty \right) $ Решите неравенство $2\log _2 (x)+\log _2 \left (x+\frac{1}{x^2}\right)\leq 2\log _2 \left (\frac{x^2+x}{2} \right) $.
1. $\left [ \frac{-5+\sqrt{41}}{8}; \frac{1}{2} \right) $ Решите неравенство $\log _3 (1-2x)-\log _3 \left (\frac{1}{x}-2\right)\leq \log _3 (4x^2+6x-1) $.
1. $\left [ \frac{1}{6}; \frac{1}{2} \right) $ Решите неравенство $2\log _2 (1-2x)-\log _2 \left (\frac{1}{x}-2\right)\leq \log _2 (4x^2+6x-1) $.
1. $(1; +\infty) $ Решите неравенство $\log _2 (x-1)+\log _2 \left (2x+\frac{4}{x-1}\right)\geq \log _2 \left (\frac{3x-1}{2} \right) $.
1. $\left [ \frac{11+3\sqrt{17}}{2}; +\infty \right) $ Решите неравенство $\log_2 (4x^2-1) -\log_2 x \leq \log_2 \left (5x+\frac{9}{x}-11 \right) $.

18 : Уравнения, неравенства, системы с параметром

1. $$ \left (-\frac{4}{3}; -\frac{3}{4}\right) \cup \left (\frac{3}{4}; 1\right)\cup \left (1; \frac{4}{3}\right)$$
  $\left\{\begin{matrix}\begin{array}{lcl} (x+ay-5)(x+ay-5a)=0 \\ x^2+y^2=16 \end{array}\end{matrix}\right. $
2. $$ \left (-\frac{3\sqrt{7}}{7}; -\frac{\sqrt{7}}{3}\right) \cup \left (\frac{\sqrt{7}}{3}; 1\right)\cup \left (1; \frac{3\sqrt{7}}{7}\right)$$
  $\left\{\begin{matrix}\begin{array}{lcl} (x+ay-4)(x+ay-4a)=0 \\ x^2+y^2=9 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
3. $$ \left (-\frac{3\sqrt{5}}{2}; -\frac{2\sqrt{5}}{15}\right) \cup \left (\frac{2\sqrt{5}}{15}; 1\right)\cup \left (1; \frac{3\sqrt{5}}{2}\right)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} (x+ay-7)(x+ay-7a)=0 \\ x^2+y^2=45 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
4. $$ \left (-2\sqrt{2}; -\frac{\sqrt{2}}{4}\right) \cup \left (\frac{\sqrt{2}}{4}; 1\right)\cup \left (1; 2\sqrt{2} \right)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} (x+ay-3)(x+ay-3a)=0 \\ x^2+y^2=8 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$ (1-\sqrt{2}; 0) \cup (0; 1.2) \cup (1.2; 3\sqrt{2}-3) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2+2(a-3)x-4ay+5a^2-6a=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
2. $$ (4-3\sqrt2; 1-\frac{2}{\sqrt5}) \cup (1-\frac{2}{\sqrt5}; 1+\frac{2}{\sqrt5}) \cup (\frac{2}{3}+\sqrt2; 4+3\sqrt2) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2-4ax+6x-(2a+2)y+5a^2-10a+1=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
3. $$ \left (-\frac{2+\sqrt{2}}{3}; -1 \right)\cup (-1; -0.6) \cup (-0.6; \sqrt{2}-2) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2-4(a+1)x-2ay+5a^2+8a+3=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
4. $$ \left (\frac{2}{9}; 2 \right) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2-4(a+1)x-2ay+5a^2-8a+4=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
5. $$ \left (3-\sqrt2; \frac{8}{5} \right) \cup \left (\frac{8}{5}; 2 \right) \cup \left (2; \frac{3+\sqrt2}{ 2} \right) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2-6(a-2)x-2ay+10a^2+32-36a=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
6. $$ (1-\sqrt2; 0) \cup (0; 0.8) \cup (0.8; 2\sqrt2-2) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^2+y^2-2(a-4)x-6ay+10a^2-8a=0 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$ (2; 4)\cup (6; +\infty)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4-y^4=10a-24 \\ x^2+y^2=a \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
2. $$ (2; 6-2\sqrt{2})\cup(6+2\sqrt{2};+\infty) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4-y^4=12a-28 \\ x^2+y^2=a \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$ \left (-\frac{3}{14}(\sqrt2-4); \frac{3}{5} \right ]\cup \left [ 1; \frac{3}{14}(\sqrt2+4) \right) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4+y^2=a^2 \\ x^2+y=|4a-3| \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
2. $$ (4-2\sqrt{2};\frac{4}{3})\cup(4;4+2\sqrt{2}) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4+y^2=a^2 \\ x^2+y=|2a-4| \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
3. $$ (5-\sqrt{2};4)\cup (4;5+\sqrt{2})$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4+y^2=2a-7 \\ x^2+y=|a-3| \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
4. $$ \left (\frac{1}{7}(4-\sqrt2); \frac{2}{5} \right) \cup \left (\frac{2}{5}; \frac{1}{2} \right) \cup \left (\frac{1}{2} ; \frac{1}{7}(\sqrt2+4) \right) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} x^4+y^2=a^2 \\ x^2+y=|4a-2| \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$ \left (\frac{-2-\sqrt{2}}{3}; -1 \right)\cup (-1; -0.6)\cup (-0.6; \sqrt{2}-2) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} (x-(2a+2))^2+(y-a)^2=1 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
2. $$(1-\sqrt{2}; 0)\cup(0; 1.2) \cup (1.2; 3\sqrt{2}-3) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} (x-(3-a))^2+(y-2a)^2=9 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$(-9.25; -3)\cup (-3;3)\cup (3; 9.25)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} y=(a+3)x^2+2ax+a-3 \\ x^2=y^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
2. $$(-4.25;-2)\cup(-2;2)\cup(2;4,25)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} y=(a+2)x^2-2ax+a-2 \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
3. $$(-4.25; -2)\cup (-2;2)\cup (2; 4.25)$$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} y=(a-2)x^2-2ax-2+a \\ y^2=x^2 \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$ (-\infty ; -3)\cup (-3; 0)\cup (3;\frac{25}{8}) $$ Найдите все значения параметра a, при каждом из которых система
  $\left\{\begin{matrix}\begin{array}{lcl} ax^2+ay^2-(2a-5)x+2ay+1=0 \\ x^2+y=xy+x \end{array}\end{matrix}\right. $
  Уравнений имеет ровно четыре различных решения.
1. $$\left [ 0; \frac{2}{3} \right ]$$ Найдите все значения параметра a, при каждом из которых уравнение
  $\sqrt{x+2a-1}+\sqrt{x-a}=1 $
  Имеет хотя бы одно решение.